Constraints in the E/R Model
Constraints in the E/R Model
- The E/R model provides ways to express common data constraints, similar to the relational model.
- An arrow connecting a relationship to an entity set represents a “functional dependency.”
- A referential-integrity constraint requires an entity in one set to be related to an entity in another set.
#1
read: Section 4.3: Constraints in the E/R Model (section)
model: pro
rules: bullet definition math presentation short
Present the following. Use definition formal definition when it applies.
- The E/R model provides ways to express common data constraints, similar to the relational model.
- An arrow connecting a relationship to an entity set represents a "functional dependency."
- A referential-integrity constraint requires an entity in one set to be related to an entity in another set.
The Entity-Relationship model incorporates several methods for expressing constraints on the data, analogous to the constraints found in the relational model. These mechanisms ensure the integrity and logical consistency of the database design.
Constraints on Data
The E/R model allows for the specification of common constraints that will populate the database. This includes defining keys for entity sets, functional dependencies through relationships, and referential integrity.
Functional Dependencies
An arrow connecting a relationship to an entity set indicates a functional dependency. Specifically, if an arrow points from a relationship \(R\) to an entity set \(E\), it signifies that each entity in the other participating entity sets is related to at most one entity in \(E\). This is a many-one constraint.
Referential Integrity
A referential-integrity constraint mandates that an entity in one set must be related to an existing entity in another set. In E/R diagrams, this is often represented by a rounded arrowhead, which combines the many-one constraint with a participation constraint, indicating that the relationship is mandatory.
Let \(E\) be an entity set. A key for \(E\) is a set of one or more attributes \(K\) such that for any two distinct entities \(e_1, e_2 \in E\), it is not possible for \(e_1\) and \(e_2\) to have identical values for each of the attributes in \(K\).
Formally, let \(\pi_K(e)\) denote the values of the attributes in \(K\) for an entity \(e\). Then for any \(e_1, e_2 \in E\):
\[ \text{if } e_1 \neq e_2, \text{ then } \pi_K(e_1) \neq \pi_K(e_2) \]
- Version: 1
- Model: gemini-2.5-pro
- Created: 2025-09-25 18:17:11
- Duration: 15.01069712638855
- Cummulative cost: $1.67e-02
Keys in the E/R Model
- A key for an entity set \(E\) is a set of attributes \(K\) such that no two distinct entities \(e_1\) and \(e_2\) in \(E\) can have identical values for all attributes in \(K\).
- Every entity set must have a key, though for ‘weak’ entity sets or in
isa-hierarchies, the key may belong to another entity set. - An entity set can have multiple possible keys, but it is customary to select one as the “primary key.”
- In an
isa-hierarchy, the root entity set must possess all attributes needed for a key.
#2
read: Section 4.3.1: Keys in the E/R Model (section)
model: pro
rules: bullet definition math presentation short
Present the following. Use definition formal definition when it applies.
- A key for an entity set $E$ is a set of attributes $K$ such that no two distinct entities $e_1$ and $e_2$ in $E$ can have identical values for all attributes in $K$.
- Every entity set must have a key, though for 'weak' entity sets or in `isa`-hierarchies, the key may belong to another entity set.
- An entity set can have multiple possible keys, but it is customary to select one as the "primary key."
- In an `isa`-hierarchy, the root entity set must possess all attributes needed for a key.
Let \(E\) be an entity set. A key for \(E\) is a set of one or more attributes \(K\) such that for any two distinct entities \(e_1 \in E\) and \(e_2 \in E\), it is not possible for \(e_1\) and \(e_2\) to have identical values for each of the attributes in the key \(K\).
Every entity set is required to have a key.
In certain cases, such as
isa-hierarchies and “weak” entity sets, the key for an entity set may be composed of attributes from another, related entity set.An entity set may have more than one possible key.
It is conventional to designate one of these keys as the “primary key.” The design then proceeds as if this were the only key for the entity set.
In an
isa-hierarchy, the key for any entity within the hierarchy is determined by the key of the root entity set.The root of the hierarchy must possess all attributes necessary to form a key. This key is used to uniquely identify entities throughout the hierarchy, regardless of their specific subtype.
- Version: 1
- Model: gemini-2.5-pro
- Created: 2025-09-25 18:17:25
- Duration: 13.270258903503418
- Cummulative cost: $1.49e-02
Representing Keys in the E/R Model
- In E/R diagrams, attributes that form a key for an entity set are underlined.
- If multiple attributes form the key, they are all underlined.
- The notation does not support representing multiple candidate keys; only the primary key is underlined.
- The concept of “weak entity sets” is introduced, where key attributes might not belong to the entity set itself.
#3
read: Section 4.3.2: Representing Keys in the E/R Model (section)
model: pro
rules: bullet definition math presentation short
Present the following. Use definition formal definition when it applies.
- In E/R diagrams, attributes that form a key for an entity set are underlined.
- If multiple attributes form the key, they are all underlined.
- The notation does not support representing multiple candidate keys; only the primary key is underlined.
- The concept of "weak entity sets" is introduced, where key attributes might not belong to the entity set itself.
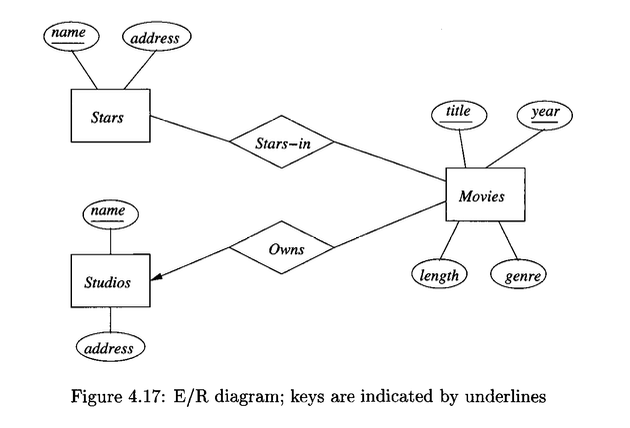
In our E/R-diagram notation, we specify the keys for an entity set by underlining the attributes that form the key.
Key Attribute Indication
The attributes belonging to the chosen key for an entity set are underlined. This provides a clear, graphical representation of the unique identifier for entities within that set. For example, the
nameattribute is underlined for theStarsandStudiosentity sets.Composite Keys
If a key consists of more than one attribute, all attributes forming the key are underlined. This signifies that the combination of these attributes must be unique. For the
Moviesentity set, bothtitleandyearare underlined to indicate they jointly form the key.Primary Key Representation
The diagrammatic convention is to underline only the attributes of the primary key. The E/R model provides no standard notation for representing multiple candidate keys for a single entity set.
Weak Entity Sets
In some circumstances, the attributes forming the key for an entity set may not all be attributes of the entity set itself. Such a set is termed a “weak entity set,” a concept to be discussed in greater detail subsequently.
- Version: 1
- Model: gemini-2.5-pro
- Created: 2025-09-25 18:17:41
- Duration: 16.243093967437744
- Cummulative cost: $1.65e-02
This is an E/R diagram with keys.
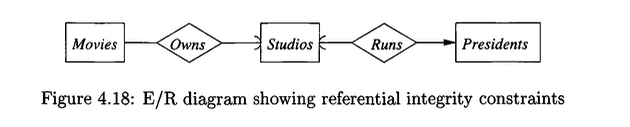
Referential Integrity
- Referential integrity constraints dictate that a value in one context must also exist in another.
- In E/R diagrams, a rounded arrowhead pointing from a relationship \(R\) to an entity set \(F\) indicates not only a many-one relationship from another entity set \(E\) to \(F\), but also that the related entity in \(F\) must exist.
- This notation enforces that for a given entity in \(E\), its corresponding entity in \(F\) via relationship \(R\) is mandatory.
#4
read: Section 4.3.3: Referential Integrity (section)
model: pro
rules: bullet definition math presentation short
Present the following. Use definition formal definition when it applies.
- Referential integrity constraints dictate that a value in one context must also exist in another.
- In E/R diagrams, a rounded arrowhead pointing from a relationship $R$ to an entity set $F$ indicates not only a many-one relationship from another entity set $E$ to $F$, but also that the related entity in $F$ must exist.
- This notation enforces that for a given entity in $E$, its corresponding entity in $F$ via relationship $R$ is mandatory.
Referential integrity constraints ensure that a value appearing in one context must also be present in another. In the Entity-Relationship model, this concept is crucial for maintaining data consistency, particularly when one entity’s existence depends on another.
Let \(R\) be a relationship from an entity set \(E\) to an entity set \(F\). A referential integrity constraint on this relationship mandates that for each entity \(e \in E\), the entity \(f \in F\) referenced by \(e\) through \(R\) must exist in the database.
- Constraint Representation
In E/R diagrams, a referential integrity constraint is represented by a rounded arrowhead. This symbol combines a cardinality constraint with an existence requirement.
- Interpretation of the Rounded Arrowhead
A rounded arrowhead pointing from a relationship diamond \(R\) to an entity set \(F\) indicates two conditions:
- The relationship is many-one from any other participating entity set \(E\) to \(F\). That is, an entity in \(E\) can be related to at most one entity in \(F\).
- The participation of \(E\) in the relationship is total. For every entity in \(E\), the corresponding entity in \(F\) to which it is related is required to exist. This is equivalent to a cardinality constraint of exactly one (\(=1\)).
- Version: 1
- Model: gemini-2.5-pro
- Created: 2025-09-25 18:17:55
- Duration: 13.4846932888031
- Cummulative cost: $1.44e-02
Degree Constraints
- Degree constraints in the E/R model allow for bounding the number of entities that can be connected to any single entity via a relationship.
- This is represented by attaching a bounding number (e.g.,
<= 10) to the edge connecting a relationship to an entity set. - The standard arrow notation can be viewed as a degree constraint: a pointed arrow is equivalent to
$<= 1and a rounded arrow is equivalent to= 1.
#5
read: Section 4.3.4: Degree Constraints (section)
model: pro
rules: bullet definition math presentation short
Present the following. Use definition formal definition when it applies.
- Degree constraints in the E/R model allow for bounding the number of entities that can be connected to any single entity via a relationship.
- This is represented by attaching a bounding number (e.g., `<= 10`) to the edge connecting a relationship to an entity set.
- The standard arrow notation can be viewed as a degree constraint: a pointed arrow is equivalent to `$<= 1` and a rounded arrow is equivalent to `= 1`.
Degree constraints in the E/R model provide a mechanism to specify bounds on the number of entities from one entity set that can be related to a single entity from another entity set via a particular relationship.
Let \(R\) be a relationship set involving an entity set \(E\). A degree constraint on the participation of \(E\) in \(R\) is a numerical bound (e.g., min, max, or an exact number) on the number of relationships in \(R\) in which any single entity \(e \in E\) can participate.
In E/R diagrams, a degree constraint is represented by attaching a label indicating the bound to the edge connecting a relationship to an entity set.
For example, to constrain a movie to have no more than 10 stars, a label such as
$<= 10$is placed on the edge from the relationshipStars-into the entity setStars. This limits the number ofStarsentities that can be connected to any singleMoviesentity.The standard arrow notations for many-one relationships are special cases of degree constraints.
A simple pointed arrow is a synonym for the constraint \(<= 10\). It indicates that an entity from the “many” side can be related to at most one entity from the “one” side. A rounded arrow, which also implies referential integrity, stands for the constraint \(= 1\), indicating that an entity must be related to exactly one other entity.
- Version: 1
- Model: gemini-2.5-pro
- Created: 2025-09-25 18:18:07
- Duration: 12.380977153778076
- Cummulative cost: $1.24e-02

